#14707
#14707: При решении задачи коммивояжера методом ветвей и границ, верно, что:
При решении задачи коммивояжера методом ветвей и границ, верно, что:
Варианты ответа:
- при запрете переезда из города i в город j на пересечении i-ой строки и j-ого столбца ставят ноль;
- запрет переезда из одного города в другой осуществляется вычеркиванием из матрицы соответствующей строки и столбца;
-
для того, чтобы запретить переезд (i, j) (i=j) необходимо на пересечении i-ой строки и j-ого столбца матрицы поставить
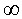
Тематика:
Исследование операций в экономике
Курсы в категории:
Экономика и управление
Данная дисциплина изучает методы математического моделирования и анализа для принятия оптимальных решений в экономике и управлении. Она охватывает инструменты линейного и нелинейного программирования, теорию игр, методы анализа рисков и управления ресурсами. Основная цель — научить находить рациональные решения в условиях ограничений, повышая эффективность бизнес-процессов и минимизируя затраты. Применение этих методов позволяет улучшать стратегическое планирование и адаптироваться к изменяющимся рыночным условиям.
Данная дисциплина изучает методы математического моделирования и анализа для принятия оптимальных решений в экономике и управлении. Она охватывает инструменты линейного и нелинейного программирования, теорию игр, методы анализа рисков и управления ресурсами. Основная цель — научить находить рациональные решения в условиях ограничений, повышая эффективность бизнес-процессов и минимизируя затраты. Применение этих методов позволяет улучшать стратегическое планирование и адаптироваться к изменяющимся рыночным условиям.