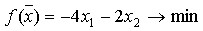#14897

#14897: Решение общей задачи линейного программирования (ОЗЛП) существует:

Решение общей задачи линейного программирования (ОЗЛП) существует:

Варианты ответа:

всегда
не всегда

🔒 Ответ будет доступен после оплаты

Тематика: Математические методы исследования операций

Курс направлен на изучение фундаментальных принципов и современных методов анализа данных, включая сбор, обработку и интерпретацию информации. Рассматриваются ключевые алгоритмы машинного обучения, статистические модели и инструменты визуализации. Особое внимание уделяется практическому применению навыков для решения реальных задач в различных областях. Программа подходит как для начинающих, так и для специалистов, желающих углубить свои знания.

Курс направлен на изучение фундаментальных принципов и современных методов анализа данных, включая сбор, обработку и интерпретацию информации. Рассматриваются ключевые алгоритмы машинного обучения, статистические модели и инструменты визуализации. Особое внимание уделяется практическому применению навыков для решения реальных задач в различных областях. Программа подходит как для начинающих, так и для специалистов, желающих углубить свои знания.

Похожие вопросы по дисциплине

📚 Похожие вопросы по этой дисциплине

В задаче линейного программирования целевая функция имеет вид. Вектор-градиент на графике в таком случае направлен:

Дана задача: Оптика выпускает 3 вида продукции: обыкновенные очки, солнцезащитные очки и контактные линзы. Для производства используются 3 вида сырья: A, B, C. Расходы сырья приведены в таблице:

Дана задача: На фабрике мягких игрушек выпускаются следующие виды изделий: медвежонок, тигр, лошадь, заяц. Ресурсы фабрики: рабочая сила – 50 чел.-дн.; сырье – 500 кг; оборудование – 200 станко-ч. Затраты ресурсов на выпуск 1 единицы продукции отражены в таблице:

Дана задача: Завод выпускает 3 вида мотоциклов: кроссовый, спортивный, грузовой. Для их изготовления используется сырье 3 типов: S1,S2,S3, где: S1 – сталь; S2 – резина; S3 – пластмасса. Норма расхода каждого из видов сырья на 1 мотоцикл и объем расхода сырья на 1 день приведены в таблице:

Дана задача: Завод выпускает машины: легковые и грузовые. В год на рынке может быть реализовано до 2000 машин. Для каждой легковой машины требуется 200 м2 материала, для грузовых – 900 м2 материала. В неделю завод получает 1000 м2 материала. Для изготовления и комплектации одной легковой машины требуется 30 часов работы цехов, а для грузовой машины требуется 49 часов работы цехов. Оборудование в цехах можно использовать 300 часов в неделю. Прибыль от продажи одной легковой машины составляет 1900 долларов, а грузовой – 2200 долларов. Математическая модель максимизации прибыли представляет собой: