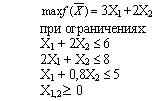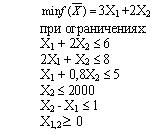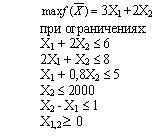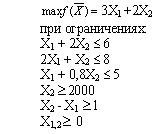#14956
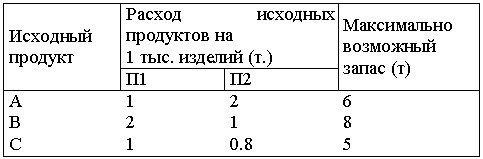
#14956: Дана задача: Фабрика выпускает продукцию двух видов: П1 и П2. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта - A, B, C. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно. Расходы сырья A, B, C на 1 тыс. изделий П1 и П2 приведены в таблице. Изучение рынка сбыта показало, что суточный спрос на изделия П2 никогда не превышает спроса изделия П1 более чем на 1 тыс. шт. Кроме того, установлено, что спрос на изделия П2 никогда не превышает 2 тыс. шт. в сутки. Оптовые цены 1 тыс. шт. изделий П1 равны 3 тыс. руб., 1 тыс. шт. П2 - 2 тыс. шт. Математическая модель максимизации дохода представляет собой: /images/00001-10000/00483/00483-718.jpg
Дана задача: Фабрика выпускает продукцию двух видов: П1 и П2. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта - A, B, C. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно. Расходы сырья A, B, C на 1 тыс. изделий П1 и П2 приведены в таблице. Изучение рынка сбыта показало, что суточный спрос на изделия П2 никогда не превышает спроса изделия П1 более чем на 1 тыс. шт. Кроме того, установлено, что спрос на изделия П2 никогда не превышает 2 тыс. шт. в сутки. Оптовые цены 1 тыс. шт. изделий П1 равны 3 тыс. руб., 1 тыс. шт. П2 - 2 тыс. шт. Математическая модель максимизации дохода представляет собой:

Варианты ответа:
🔒 Ответ будет доступен после оплаты
Курс направлен на изучение фундаментальных принципов и современных методов анализа данных, включая сбор, обработку и интерпретацию информации. Рассматриваются ключевые алгоритмы машинного обучения, статистические модели и инструменты визуализации. Особое внимание уделяется практическому применению навыков для решения реальных задач в различных областях. Программа подходит как для начинающих, так и для специалистов, желающих углубить свои знания.
Курс направлен на изучение фундаментальных принципов и современных методов анализа данных, включая сбор, обработку и интерпретацию информации. Рассматриваются ключевые алгоритмы машинного обучения, статистические модели и инструменты визуализации. Особое внимание уделяется практическому применению навыков для решения реальных задач в различных областях. Программа подходит как для начинающих, так и для специалистов, желающих углубить свои знания.
Похожие вопросы по дисциплине
📚 Похожие вопросы по этой дисциплине
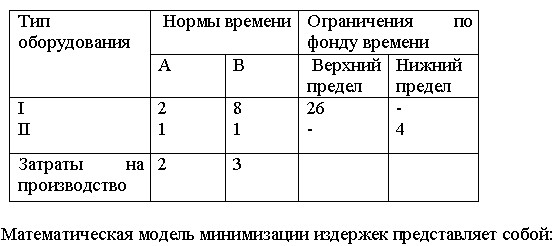
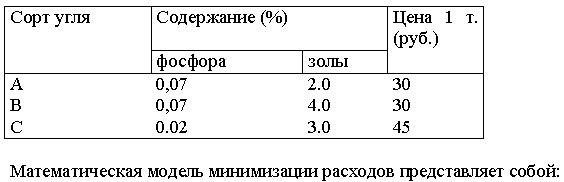
Дана задача: Компания специализируется на производстве технических лаков. Представленная ниже таблица содержит информацию о ценах продажи и соответствующих издержках производства единицы полировочного и матового лаков. Дана задача: В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено 19.3 м2-площади. На приобретение оборудования предприятие может израсходовать 10 тыс. у.е., при этом оно может купить оборудование двух видов. Комплект оборудования 1 вида стоит 1000 у.е., а II вида—3000 у.е. Приобретение одного комплекта обору¬дования 1 вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования II вида — на 3 ед. Зная, что для установки одного комплекта оборудования 1 вида требу¬ется 2 м2 площади, а оборудования II вида — 1 м2 площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции. Математическая модель максимизации дохода представляет собой: Дана задача: Для производства двух видов изделий А и В используется два типа технологического оборудования. Известны затраты времени и других ресурсов на производство ед. изделия каждого вида (см. табл.)