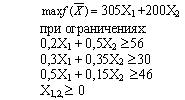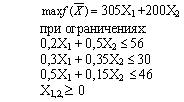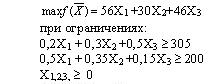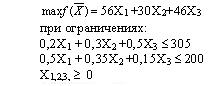#189123
#189123: Дана задача: Из трех сортов муки образуются две смеси. Первая состоит из 20% муки первого сорта, 30% муки 2-го сорта, 50% муки 3-го сорта; вторая – 50% - 1-го, 35 % - 2-го, 15 % - 3-го сорта. Доход от продажи 1-ой смеси - 305 у.е., второй - 200 у.е. за тонну. Запасы муки составляют: 56 тонн 1-го сорта, 30 тонн 2-го сорта и 46 тонн 3-го сорта. Математическая модель максимизации дохода представляет собой:
Дана задача: Из трех сортов муки образуются две смеси. Первая состоит из 20% муки первого сорта, 30% муки 2-го сорта, 50% муки 3-го сорта; вторая – 50% - 1-го, 35 % - 2-го, 15 % - 3-го сорта. Доход от продажи 1-ой смеси - 305 у.е., второй - 200 у.е. за тонну. Запасы муки составляют: 56 тонн 1-го сорта, 30 тонн 2-го сорта и 46 тонн 3-го сорта. Математическая модель максимизации дохода представляет собой:
Варианты ответа:
🔒 Ответ будет доступен после оплаты
Дисциплина изучает методы анализа и принятия оптимальных решений в условиях ограниченных ресурсов с применением математических моделей и алгоритмов. Рассматриваются задачи линейного, нелинейного и динамического программирования, теория игр, сетевые модели и стохастические методы. Полученные знания позволяют повышать эффективность процессов в экономике, логистике, управлении проектами и других областях, где требуется рациональное распределение ресурсов. Особое внимание уделяется практическому применению оптимизационных подходов для решения реальных задач.
Дисциплина изучает методы анализа и принятия оптимальных решений в условиях ограниченных ресурсов с применением математических моделей и алгоритмов. Рассматриваются задачи линейного, нелинейного и динамического программирования, теория игр, сетевые модели и стохастические методы. Полученные знания позволяют повышать эффективность процессов в экономике, логистике, управлении проектами и других областях, где требуется рациональное распределение ресурсов. Особое внимание уделяется практическому применению оптимизационных подходов для решения реальных задач.