Для придания компактности формулам, с помощью которых строится граница эффективных портфелей, У. Шарп предложил ввести понятие (n+1)-ой акции портфеля. Тогда нужно учитывать дисперсию случайной ошибки этой (n+1)-ой акции:
🧠 Тематика вопроса:
Данная дисциплина изучает фундаментальные принципы и методы анализа данных, включая сбор, обработку и интерпретацию информации. Рассматриваются современные инструменты и технологии, применяемые в машинном обучении, статистике и визуализации данных. Особое внимание уделяется практическому применению знаний для решения реальных задач в различных областях. Курс развивает навыки критического мышления и работы с большими массивами информации, что необходимо для успешной деятельности в условиях цифровой экономики.
Варианты ответа:
- нет, поскольку такая дисперсия вообще не вводится в модели У. Шарпа;
- да, и такая дисперсия равняется взвешенной величине дисперсий случайных ошибок акций рыночного портфеля
- да, и дисперсия ошибки (n+1)-ой акции портфеля подсчитывается как взвешенная величина дисперсий случайных ошибок акций исследуемого портфеля
-
да, и дисперсия ошибки (n+1)-ой акции портфеля равняется дисперсии доходности рыночного портфеля
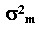
Ответ будет доступен после оплаты