#206005
#206005: Если уравнение второго порядка для функции u в данной точке (х, у) принадлежит к эллиптическому типу, то дискриминант В2–АС удовлетворяет соотношению
Если уравнение второго порядка для функции u в данной точке (х, у) принадлежит к эллиптическому типу, то дискриминант В2–АС удовлетворяет соотношению
Варианты ответа:
- В2–АС=0
- В2–АС>0
- В2–АС
-
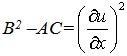
🔒 Ответ будет доступен после оплаты
Тематика:
Уравнения математической физики
Дисциплина направлена на изучение ключевых принципов и методов, необходимых для понимания основных процессов и закономерностей. В рамках курса рассматриваются современные подходы, инструменты и технологии, позволяющие анализировать и решать практические задачи. Особое внимание уделяется развитию навыков критического мышления, работы с информацией и применения полученных знаний в профессиональной деятельности. Программа включает теоретические модули, практические задания и кейсы для самостоятельной работы.
Дисциплина направлена на изучение ключевых принципов и методов, необходимых для понимания основных процессов и закономерностей. В рамках курса рассматриваются современные подходы, инструменты и технологии, позволяющие анализировать и решать практические задачи. Особое внимание уделяется развитию навыков критического мышления, работы с информацией и применения полученных знаний в профессиональной деятельности. Программа включает теоретические модули, практические задания и кейсы для самостоятельной работы.