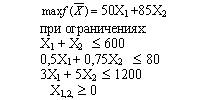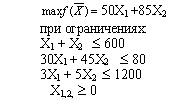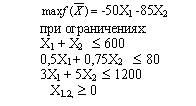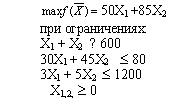#43216
#43216: Дана задача: Фирма производит одежду двух видов: платья и костюмы. В неделю фирма продает не более 600 изделий. Для каждого платья требуется 3 м полотна, а для костюма 5 м. Фирма в неделю получает 1200 м полотна. Для шитья 1 платья требуется 30 минут, а для шитья костюма 45 минут. Оборудование может использоваться не больше 80 часов в неделю. Если прибыль от продаж платья – 50$, то от костюма – 85$. Математическая модель максимизации прибыли представляет собой:
Дана задача: Фирма производит одежду двух видов: платья и костюмы. В неделю фирма продает не более 600 изделий. Для каждого платья требуется 3 м полотна, а для костюма 5 м. Фирма в неделю получает 1200 м полотна. Для шитья 1 платья требуется 30 минут, а для шитья костюма 45 минут. Оборудование может использоваться не больше 80 часов в неделю. Если прибыль от продаж платья – 50$, то от костюма – 85$. Математическая модель максимизации прибыли представляет собой:
Варианты ответа:
🔒 Ответ будет доступен после оплаты
Дисциплина изучает методы анализа и принятия оптимальных решений в условиях ограниченных ресурсов с применением математических моделей и алгоритмов. Рассматриваются задачи линейного, нелинейного и динамического программирования, теория игр, сетевые модели и стохастические методы. Полученные знания позволяют повышать эффективность процессов в экономике, логистике, управлении проектами и других областях, где требуется рациональное распределение ресурсов. Особое внимание уделяется практическому применению оптимизационных подходов для решения реальных задач.
Дисциплина изучает методы анализа и принятия оптимальных решений в условиях ограниченных ресурсов с применением математических моделей и алгоритмов. Рассматриваются задачи линейного, нелинейного и динамического программирования, теория игр, сетевые модели и стохастические методы. Полученные знания позволяют повышать эффективность процессов в экономике, логистике, управлении проектами и других областях, где требуется рациональное распределение ресурсов. Особое внимание уделяется практическому применению оптимизационных подходов для решения реальных задач.