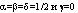#51574
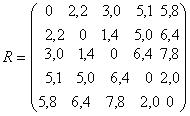
#51574: В задачах многомерной классификации объектов при расстояние между классами определяется по принципу … /images/00001-10000/01683/01683-67.jpg
В задачах многомерной классификации объектов при расстояние между классами определяется по принципу …
Варианты ответа:
- “дальнего соседа”
- “средней связи”
- “ближайшего соседа”
🔒 Ответ будет доступен после оплаты
Тематика:
Эконометрика
Данная дисциплина направлена на изучение ключевых принципов и методов, необходимых для понимания и применения современных технологий в профессиональной деятельности. В рамках курса рассматриваются теоретические основы, практические аспекты и актуальные тенденции, позволяющие развить навыки анализа и решения сложных задач. Особое внимание уделяется междисциплинарному подходу, что способствует формированию системного мышления и умения работать в команде. Программа включает лекции, семинары и практические задания для закрепления материала.
Данная дисциплина направлена на изучение ключевых принципов и методов, необходимых для понимания и применения современных технологий в профессиональной деятельности. В рамках курса рассматриваются теоретические основы, практические аспекты и актуальные тенденции, позволяющие развить навыки анализа и решения сложных задач. Особое внимание уделяется междисциплинарному подходу, что способствует формированию системного мышления и умения работать в команде. Программа включает лекции, семинары и практические задания для закрепления материала.
Похожие вопросы по дисциплине
📚 Похожие вопросы по этой дисциплине
В задачах многомерной классификации объектов при - расстояние между классами определяется по принципу …