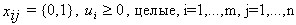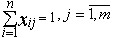#519887
#519887: Опорный план задачи линейного программирования не определяет матрица:
Опорный план задачи линейного программирования не определяет матрица:
Варианты ответа:
🔒 Ответ будет доступен после оплаты
Дисциплина изучает методы анализа и принятия оптимальных решений в условиях ограниченных ресурсов с применением математических моделей и алгоритмов. Рассматриваются задачи линейного, нелинейного и динамического программирования, теория игр, сетевые модели и стохастические методы. Полученные знания позволяют повышать эффективность процессов в экономике, логистике, управлении проектами и других областях, где требуется рациональное распределение ресурсов. Особое внимание уделяется практическому применению оптимизационных подходов для решения реальных задач.
Дисциплина изучает методы анализа и принятия оптимальных решений в условиях ограниченных ресурсов с применением математических моделей и алгоритмов. Рассматриваются задачи линейного, нелинейного и динамического программирования, теория игр, сетевые модели и стохастические методы. Полученные знания позволяют повышать эффективность процессов в экономике, логистике, управлении проектами и других областях, где требуется рациональное распределение ресурсов. Особое внимание уделяется практическому применению оптимизационных подходов для решения реальных задач.
Похожие вопросы по дисциплине
📚 Похожие вопросы по этой дисциплине
В задаче линейного программирования целевая функция имеет вид. Найдено оптимальное решение, достигаемое в точках: (0;10), (2;6). Оптимальное значение целевой функции составляет:
