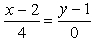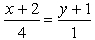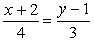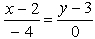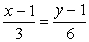#586935
#586935: Уравнение прямой, проходящей через точки А(2; 1) и B(6; 1), в каноническом виде: …
Уравнение прямой, проходящей через точки А(2; 1) и B(6; 1), в каноническом виде: …
Варианты ответа:
Тематика:
Геометрия и топология
Курсы в категории:
Математика и статистика
Данная дисциплина исследует структуры пространств, формы объектов и их преобразования, уделяя особое внимание фундаментальным свойствам и взаимосвязям. Она развивает логическое и абстрактное мышление, позволяя анализировать сложные геометрические и топологические задачи. Знания, полученные в рамках курса, находят применение в различных областях, включая теоретическую математику, физику, компьютерную графику и инженерные науки. Изучение материала способствует формированию строгого математического подхода и умения работать с многомерными и нестандартными пространствами.
Данная дисциплина исследует структуры пространств, формы объектов и их преобразования, уделяя особое внимание фундаментальным свойствам и взаимосвязям. Она развивает логическое и абстрактное мышление, позволяя анализировать сложные геометрические и топологические задачи. Знания, полученные в рамках курса, находят применение в различных областях, включая теоретическую математику, физику, компьютерную графику и инженерные науки. Изучение материала способствует формированию строгого математического подхода и умения работать с многомерными и нестандартными пространствами.