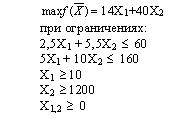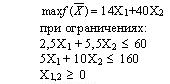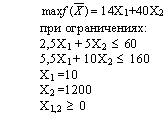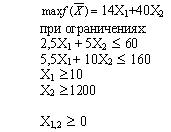#671517
#671517: Дана задача: Фирма, имеющая лесопильный завод и фабрику, на которой изготавливается фанера, столкнулась с проблемой наиболее рационального использования лесоматериалов. Чтобы получить 1 м3 комплектов пиломатериалов, необходимо израсходовать 2.5 куб. м еловых и 5.5 куб. м пихтовых лесоматериалов. Для приготовления 100 кв.м фанеры требуется 5 куб. м еловых и 10 куб. м пихтовых материалов. Фирма имеет 60 куб. м еловых и 160 куб. м пихтовых лесоматериалов. Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10 куб. м пиломатериалов и 1200 кв. м фанеры. Доход с 1 куб. м пиломатериалов составляет 14 долл., а со 100 кв. м фанеры - 40 долл. Математическая модель максимизации дохода представляет собой:
Дана задача: Фирма, имеющая лесопильный завод и фабрику, на которой изготавливается фанера, столкнулась с проблемой наиболее рационального использования лесоматериалов. Чтобы получить 1 м3 комплектов пиломатериалов, необходимо израсходовать 2.5 куб. м еловых и 5.5 куб. м пихтовых лесоматериалов. Для приготовления 100 кв.м фанеры требуется 5 куб. м еловых и 10 куб. м пихтовых материалов. Фирма имеет 60 куб. м еловых и 160 куб. м пихтовых лесоматериалов. Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10 куб. м пиломатериалов и 1200 кв. м фанеры. Доход с 1 куб. м пиломатериалов составляет 14 долл., а со 100 кв. м фанеры - 40 долл. Математическая модель максимизации дохода представляет собой:
Варианты ответа:
🔒 Ответ будет доступен после оплаты
Данная дисциплина изучает процесс принудительного исполнения судебных и иных решений, включая правовые нормы, регулирующие взыскание задолженностей. Рассматриваются механизмы защиты интересов как кредиторов, так и должников, а также роль судебных приставов в обеспечении законности. Особое внимание уделяется практическим аспектам работы с исполнительными документами, что формирует у студентов навыки, необходимые для профессиональной деятельности в юридической сфере, правоохранительных органах и службах принудительного исполнения.
Данная дисциплина изучает процесс принудительного исполнения судебных и иных решений, включая правовые нормы, регулирующие взыскание задолженностей. Рассматриваются механизмы защиты интересов как кредиторов, так и должников, а также роль судебных приставов в обеспечении законности. Особое внимание уделяется практическим аспектам работы с исполнительными документами, что формирует у студентов навыки, необходимые для профессиональной деятельности в юридической сфере, правоохранительных органах и службах принудительного исполнения.