📚
Все вопросы
- Наработка технической системы до отказа описывается экспоненциальным распределением с параметром λ = 10^-4[1/ч]. Определить плотность распределения наработки до отказа системы ω(t) за время работы t = 2000 [ч]. #321
-
Как определяется среднее время восстановления автоматизированной системы с вероятностью безотказной работы pв(t) = 1-e^μt в соответствии с экспоненциальным распределением?
 #322
#322
- Какие свойства включает в себя надежность автоматизированной системы? #323
-
Плотность распределения наработки до отказа системы представлена суммой экспоненциальных распределений ω1(t) и ω2(t) ω(t) = c1ω1(t) + c2ω2(t), где c1, c2 - коэффициенты веса: c1 + c2 = 1. Чему равна наработка на отказ этой системы?
 #324
#324
-
Как определяется среднее время безотказной работы системы в соответствии с гамма-распределением r, λ0
 #325
#325
-
Как определяется плотность времени восстановления автоматизированной системы в соответствии с экспоненциальным распределением?
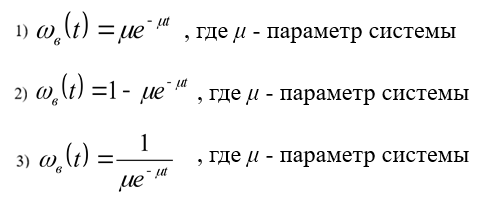 #326
#326
- Какое распределение используют для характеристики непрерывной случайной величины? #327
- Что подразумевает апостериорный анализ надежности автоматизированной системы? #328
- Наработка технической системы до отказа описывается экспоненциальным распределением с параметром λ = 10^-4[1/ч]. Определить среднюю наработку на отказ системы #329
-
На испытание поставлено 1000 однотипных элементов автоматизированной системы. За первые 3000ч отказало 80 элементов, а на интервале времени 3000-4000ч отказало еще 50 элементов. Определить статистическую оценку надежности блоков для t = 3500ч
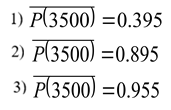 #330
#330