📚
Все вопросы
-
Если функция задана таблицей своих значений в точках, то многочлен Лагранжа … степени можно построить по этой таблице, используя все значения функции
 #31
#31
- Форма записи интерполяционного многочлена первой степени, которая соответствует многочлену Лагранжа, - … #32
- Для погрешности интерполяции многочленом Лагранжа первой степени справедлива оценка: … #33
-
У числа = 0,089600 значащие цифры - …
 #34
#34
- Интерполирование многочленом Лагранжа 2-ой степени обеспечивает порядок … точности по h #35
- Если известны значения функции в 7-ми точках, то многочлен Ньютона … степени можно построить, используя все значения функции #36
-
Функция приближается интерполяционным многочленом Ньютона 1-й степени по узлам xi, xi+1, тогда коэффициент при старшей степени x: …
 #37
#37
- Функция задана своими значениями в узлах x0, x1, …, xn, по этим значениям построены интерполяционные многочлены Ньютона Nn(x) и Лагранжа Ln(x), тогда … #38
-
Функция задана своими значениями в узлах, по этим значениям построены интерполяционные многочлены Ньютона и Лагранжа с оценкой погрешности интерполяции и соответственно; тогда …
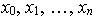 #39
#39
- Конечная разность вперед 1-го порядка определяется следующим образом: … #40