При составлении регрессионного уравнения в модели У. Шарпа для какой-то акции i получилось, что ожидаемая величина случайной ошибки Это означает, что:


🧠 Тематика вопроса:
Данная дисциплина изучает фундаментальные принципы и методы анализа данных, включая сбор, обработку и интерпретацию информации. Рассматриваются современные инструменты и технологии, применяемые в машинном обучении, статистике и визуализации данных. Особое внимание уделяется практическому применению знаний для решения реальных задач в различных областях. Курс развивает навыки критического мышления и работы с большими массивами информации, что необходимо для успешной деятельности в условиях цифровой экономики.
Варианты ответа:
- величины, соответствующие теоретическому значению доходности ri данной акции, превосходят практические значения ri/sub>на 50%
- величины, соответствующие практическому значению доходности ri данной акции, превосходят теоретические значения ri/sub> на 50%
- такого не может быть
- доходности данной акции и рыночного портфеля связаны положительной корреляцией
Ответ будет доступен после оплаты
📚 Похожие вопросы по этой дисциплине
-
В общем случае ожидаемая доходность случайной ошибки любой акции портфеля = 0. Тогда можно утверждать, что и дисперсия случайной ошибки для любой акции портфеля в модели Шарпа также равна нулю в общем случае:
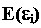
-
С помощью показателя можно оценить степень точности регрессионного уравнения и в случае отрицательных величин коэффициента:
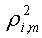
- Чем выше дисперсия случайной ошибки какой-то акции портфеля, тем точнее уравнение линейной регрессии описывает поведение ее доходности:
- Инвестор включил в портфель n акций и использует модель У. Шарпа. Для оценки риска этого портфеля ему необходимо вычислить:
- Инвестор использует модель У. Шарпа. Тогда для построения ГЭП ему необходимо вычислять дисперсии доходности каждой акции портфеля: