#751173
#751173: Для придания компактности формулам, с помощью которых строится граница эффективных портфелей, У. Шарп предложил ввести понятие (n+1)-ой акции портфеля. Тогда нужно учитывать дисперсию случайной ошибки этой (n+1)-ой акции:
Для придания компактности формулам, с помощью которых строится граница эффективных портфелей, У. Шарп предложил ввести понятие (n+1)-ой акции портфеля. Тогда нужно учитывать дисперсию случайной ошибки этой (n+1)-ой акции:
Варианты ответа:
- нет, поскольку такая дисперсия вообще не вводится в модели У. Шарпа;
- да, и такая дисперсия равняется взвешенной величине дисперсий случайных ошибок акций рыночного портфеля
- да, и дисперсия ошибки (n+1)-ой акции портфеля подсчитывается как взвешенная величина дисперсий случайных ошибок акций исследуемого портфеля
-
да, и дисперсия ошибки (n+1)-ой акции портфеля равняется дисперсии доходности рыночного портфеля
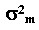
🔒 Ответ будет доступен после оплаты
Данная дисциплина изучает принципы и методы оценки инвестиционных возможностей, включая анализ финансовых активов, расчет рисков и прогнозирование доходности. В рамках курса рассматриваются инструменты для принятия взвешенных решений, направленных на оптимизацию вложений и достижение долгосрочных финансовых результатов. Особое внимание уделяется практическим аспектам управления капиталом, что позволяет применять полученные знания в реальных экономических условиях.
Данная дисциплина изучает принципы и методы оценки инвестиционных возможностей, включая анализ финансовых активов, расчет рисков и прогнозирование доходности. В рамках курса рассматриваются инструменты для принятия взвешенных решений, направленных на оптимизацию вложений и достижение долгосрочных финансовых результатов. Особое внимание уделяется практическим аспектам управления капиталом, что позволяет применять полученные знания в реальных экономических условиях.