#751294
#751294: Чем выше дисперсия случайной ошибки какой-то акции портфеля, тем точнее уравнение линейной регрессии описывает поведение ее доходности:
Чем выше дисперсия случайной ошибки какой-то акции портфеля, тем точнее уравнение линейной регрессии описывает поведение ее доходности:
Варианты ответа:
- нет, так как в этом случае уравнение регрессии менее точно описывает такое поведение
- да
-
это справедливо только для случая высоких значений коэффициентов
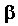
- это наблюдается, когда дисперсия случайной ошибки распределена по нормальному закону
🔒 Ответ будет доступен после оплаты
Данная дисциплина изучает принципы и методы оценки инвестиционных возможностей, включая анализ финансовых активов, расчет рисков и прогнозирование доходности. В рамках курса рассматриваются инструменты для принятия взвешенных решений, направленных на оптимизацию вложений и достижение долгосрочных финансовых результатов. Особое внимание уделяется практическим аспектам управления капиталом, что позволяет применять полученные знания в реальных экономических условиях.
Данная дисциплина изучает принципы и методы оценки инвестиционных возможностей, включая анализ финансовых активов, расчет рисков и прогнозирование доходности. В рамках курса рассматриваются инструменты для принятия взвешенных решений, направленных на оптимизацию вложений и достижение долгосрочных финансовых результатов. Особое внимание уделяется практическим аспектам управления капиталом, что позволяет применять полученные знания в реальных экономических условиях.