Вопросы по дисциплине:
Инфографика
Сбросить фильтр
| № | Вопрос | Действия |
|---|---|---|
| 2001 | Оператор обслуживает три линии производства, вероятности выхода из строя каждой производственной линии в течение смены соответственно равны 0,2; 0,5; 0,1. Составить закон распределения числа линий, не требующих ремонта в течение смены. Что следует предпринять? | Открыть |
| 2002 | Требуется определить, сколько различных пятизначных чисел можно составить из цифр 4, 5, 6, если четверка встречается один раз, пятерка– два раза, шестерка – два раза? Что следует предпринять, чтобы решить данную задачу? | Открыть |
| 2003 | Требуется определить, сколькими способами можно выбрать дежурного и старосту из 18 учащихся класса. Что следует предпринять, чтобы решить данную задачу? | Открыть |
| 2004 | Требуется найти вероятность того, что наугад выбранный человек — дальтоник, если выбор производится из группы, содержащей равное число мужчин и женщин, причем известно, что 5% мужчин и 0.25% женщин — дальтоники. Что следует предпринять, чтобы решить данную задачу? | Открыть |
| 2005 | Требуется найти у кого больше вероятность вытащить счастливый билет: у того, кто подошел первым, или у того, кто подошел вторым. Если среди 25 экзаменационных билетов имеется 5 счастливых и студенты подходят за билетами один за другим по очереди. Что следует предпринять, чтобы решить данную задачу? | Открыть |
| 2006 | В партии 50 деталей, в ней 5 бракованных деталей. Наугад отбирается 5 деталей. Если среди отобранных деталей нет бракованных, то партия принимается. Как найти вероятность того, что партия будет принята, если в ней 5 бракованных деталей? | Открыть |
| 2007 | В урне 5 белых и 8 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Как найти вероятность того, что оба шара будут белыми? | Открыть |
| 2008 | Приближенное значение функции y=√x, вычисленное с помощью дифференциала в точке x=3 равно: | Открыть |
| 2009 |
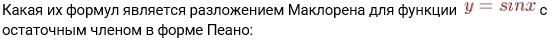
|
Открыть |
| 2010 |

|
Открыть |