📚
Все вопросы
- В общем случае, алгоритм Пауэлла – метод сопряженных направлений нулевого порядка требует: #21
- Метод Дэвидона-Флетчера-Пауэлла от метода Ньютона отличает следующее: #22
-
Линейная функция является:
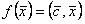 #23
#23
- Оптимум квадратичной функции Ньютона в задаче безусловной оптимизации независимо от выбора начальной точки находится за: #24
-
Направление поиска в методе Дэвидона-Флетчера-Пауэлла задается формулой:
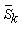 #25
#25
- Решением задачи условной оптимизации называется такой вектор, который удовлетворяет условию: #26
-
Элементы последовательности точек, монотонно увеличивающих значение функции, рассчитываются по формуле:
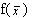 #27
#27
- В методе штрафных функций решается последовательность вспомогательных задач без ограничений: #28
-
Чтобы направление было возможным в граничной точке множества Р:
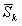 #29
#29
- Среди методов условной оптимизации к методам возможных направлений относят метод: #30