#52247

#52247: Инвестор в ходе решения задачи Г. Марковица вычислил веса акций портфеля и получил выражения вида: Тогда для построения ГЭП надо подставлять данные веса в уравнение для ожидаемой доходности портфеля и вычислять E(rrпортф. ): /images/00001-10000/01699/01699-34.jpg

Инвестор в ходе решения задачи Г. Марковица вычислил веса акций портфеля и получил выражения вида: Тогда для построения ГЭП надо подставлять данные веса в уравнение для ожидаемой доходности портфеля и вычислять E(rrпортф. ):
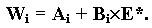
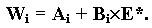
Изображение вопроса
Варианты ответа:
  • нет, достаточно подставить эти веса в выражения для дисперсий каждой акции портфеля
  • нет, достаточно подставить эти веса в выражение для дисперсии портфеля
  • это надо делать только в том случае, если при формировании портфеля используются короткие продажи
  • да, иначе нельзя построить ГЭП
Тематика: Портфельное инвестирование
📚 Похожие вопросы по этой дисциплине
Инвестор оптимизирует портфель методом Марковица, объединяя в него 3 акции. В результате у него получились следующие веса: Тогда вес третьей акции в портфеле равен:
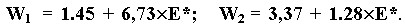
Изображение похожего вопроса
Инвестор формирует портфель из пяти акций, и для какого-то значения вес W4 принимает отрицательное значение. Инвестор не желает прибегать к коротким продажам и удаляет эту акцию из портфеля, формируя его только из четырех акций. Тогда риск портфеля из четырех акций:
Изображение похожего вопроса
Общая полезность портфеля оценивается соотношением его ожидаемой доходности и риска. Возможна ли ситуация, когда при снижении ожидаемой доходности портфеля общая полезность портфеля возрастает? Основанием для выбора инвестором оптимального портфеля из набора эффективных портфелей служит: Возможна ситуация, когда для конкретного инвестора общая полезность какого-то портфеля, соответствующего ГЭП, оказалась ниже полезности портфеля, соответствующего точке внутри области существования портфелей: