Вопросы по дисциплине:
Портфельное инвестирование
Сбросить фильтр
| № | Вопрос | Действия |
|---|---|---|
| 101 |
При составлении регрессионного уравнения в модели У. Шарпа для какой-то акции i получилось, что ожидаемая величина случайной ошибки Это означает, что: 
|
Открыть |
| 102 |
В общем случае ожидаемая доходность случайной ошибки любой акции портфеля = 0. Тогда можно утверждать, что и дисперсия случайной ошибки для любой акции портфеля в модели Шарпа также равна нулю в общем случае: 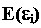
|
Открыть |
| 103 |
С помощью показателя можно оценить степень точности регрессионного уравнения и в случае отрицательных величин коэффициента: 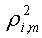
|
Открыть |
| 104 | Чем выше дисперсия случайной ошибки какой-то акции портфеля, тем точнее уравнение линейной регрессии описывает поведение ее доходности: | Открыть |
| 105 | Инвестор включил в портфель n акций и использует модель У. Шарпа. Для оценки риска этого портфеля ему необходимо вычислить: | Открыть |
| 106 | Инвестор использует модель У. Шарпа. Тогда для построения ГЭП ему необходимо вычислять дисперсии доходности каждой акции портфеля: | Открыть |
| 107 | Инвестор 10.10.05г. формирует портфель из купонных облигаций на срок до 10.10.07г. В портфель включается облигация, срок погашения которой 05.06.06г. От этой облигации инвестор намерен получить доход за счет: | Открыть |
| 108 | Сокращение объемов вычислений в модели У. Шарпа объясняется тем, что: | Открыть |
| 109 | Известно, что в модели У. Шарпа ожидаемая доходность портфеля содержит две составляющие. Теоретически может возникнуть ситуация, при которой вторая составляющая доходности превзойдет по абсолютной величина первую составляющую доходности: | Открыть |
| 110 | Для придания компактности формулам, с помощью которых строится граница эффективных портфелей, У. Шарп предложил ввести понятие (n+1)-ой акции портфеля. Под этой акцией понимается: | Открыть |